七大经典排序算法总结

Posted on | In

前言

这几天有点懒散, 可能刚开学有点兴奋, 不过博客还是要继续, 今天我们来总结一下常见的七大排序算法, 排序算法在面试和笔试中都很容易被考到, 今天我们便来总结一下.本文中所有的排序默认都是从小到大

冒泡排序

  • 介绍
    冒泡排序的原理非常简单, 它重复的走过所有元素, 一次比较两个元素, 从头到尾, 这样数组中的最大元素的位置就在数组末端了, 也就是最大元素已经归位了, 剩下就是前面n-1个元素了, 我们继续重复这个操作n-2次, 这样数组就完全排序好了.代码如下:
1
2
3
4
5
6
7
8
9
10
void bubbleSort(int *p, const int n) {
  if (p == nullptr || (n <= 0))
    return;
  for (int i = 0; i < n; ++i) {
    for (int j = 0; j < n - i - 1; ++j) {
      if (p[j] > p[j + 1])
        swap(p[j], p[j + 1]);
    }
  }
}

值得多说一句的是, 针对冒泡排序有个小小的优化:记录一下最后一次数据交换发生的位置, 这个位置之后的数据显然是有序的, 然后我们记录下来, 下一次循环的时候这个位置之后的元素就不用再排序了.

显然, 冒泡排序的复杂度是O(n^2), 不过冒泡算法是稳定的算法, 也就是说对数组进行排序前后, 相同元素的相对位置不发生变化.显然, 空间复杂度是O(1), 在交换值的时候需要O(1)的额外空间.

选择排序

  • 介绍: 选择排序是直观上最明显的排序了, 它从数组中找出最小的元素, 存放到数组的起始位置, 再从剩余的元素中继续寻找最小的元素, 放到已排序序列的尾端.重复这样的操作, 直到数组完全排序.代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
void selectSort(int *p, const int n) {
  if (p == nullptr || n <= 0)
    return;
  for (int i = 0; i < n; i++) {
    int min = i;
    for (int j = i; j < n; ++j) {
      if (p[j] < p[min])
        min = j;
    }
    std::swap(p[min], p[i]);
  }
}

很显然, 选择排序的复杂度是O(n^2), 这个是不是稳定的算法是不太明确的, 实际上这个取决于我们的实现方式, 我个人觉得我的这种实现方式是稳定的, 不过在不同实现下也不一样, 纠结这个意义不大, 我们只要理解意义即可. 空间复杂度为O(1), 交换的时候需要的额外空间.

插入排序

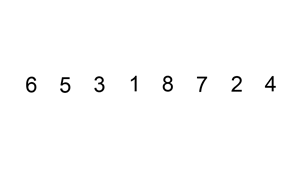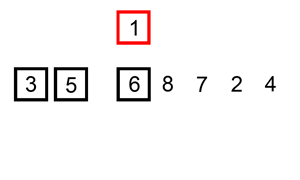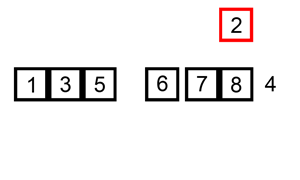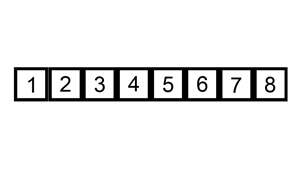
  • 介绍:插入排序的原理是对于每个未排序数据, 在已排序序列中从后向前扫描, 并找到相应位置插入. 原理也不难理解, 从数组的第一个元素开始, 这个元素可以认为是已经排序的, 取出下一个元素, 在已经排序的元素中从后向前扫描, 找到合适的位置插入该元素, 后面就是重复上面这几步, 直到元素全部有序.image

上面是我从网上找的一个gif, 可以辅助大家理解.
代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void insertSort(int *p, const int n) {
  if (p == nullptr || n <= 0)
    return;
  for (int i = 1; i < n; i++) {
    int left = i, right = i;
    int val = p[i];
    while (val < p[--left]) {
      p[right--] = p[left];
      if (left == 0)
        break;
    }
    p[right] = val;
  }
}

这里面有顺序比较操作, 所以一个可能的优化是使用二分查找来找到应该插入的位置, 这个可以提高查找的速度.

至于算法复杂度这一块, 维基百科说的很好, 我摘抄下来:
如果目标是把n个元素的序列升序排列，那么采用插入排序存在最好情况和最坏情况。最好情况就是，序列已经是升序排列了，在这种情况下，需要进行的比较操作需n-1次即可。最坏情况就是，序列是降序排列，那么此时需要进行的比较共有1/2n(n-1)次。插入排序的赋值操作是比较操作的次数减去n-1次，（因为n-1次循环中，每一次循环的比较都比赋值多一个，多在最后那一次比较并不带来赋值）。

平均来说插入排序算法复杂度为O(n^2)。因而，插入排序不适合对于数据量比较大的排序应用。但是，如果需要排序的数据量很小，例如，量级小于千；或者若已知输入元素大致上按照顺序排列，那么插入排序还是一个不错的选择。

插入排序在工业级库中也有着广泛的应用，在STL的sort算法和stdlib的qsort算法中，都将插入排序作为快速排序的补充，用于少量元素的排序（通常为8个或以下）。

对于稳定性, 显然插入排序是稳定的, 这里就不再解释了.

希尔排序

  • 介绍:
    希尔排序, 也称为递减增量排序, 实质上为分组插入排序, 希尔排序我直接用例子来解释, 这样更直观也非常容易理解:
    假设有这么一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]
    假设我们先以5为步长开始进行排序, 画出来大概如下面这样:

13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然后我们对每一列进行排序, 得到下面的结果

10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

将上述四行数字再依行的次序来连接起来, 也就是得到[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ], 然后我们再以3为步长进行排序:

10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45

排序之后就变为:

10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94

这时, 我们得到的结果是** [ 10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94**最后再以1为步长进行排序, 这个时候就是简单的插入排序了, 不过值得注意的是, 这里效率基本上肯定会比我们直接使用插入排序高不少, 因为这里的数据是有序性比较高的, 这样插入排序就会提供更高的效率.

代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void shellSort(int *p, const int length) {
  int gap, i, j;
  int temp;
  for (gap = length >> 1; gap > 0; gap >>= 1) {
    for (i = gap; i < length; i++) /* 后面是插入排序,i从gap开始是因为对于每一
          列来说第一行只有一个数字所以当然都是有序的 */
    {
      temp = p[i];
      for (j = i - gap; j >= 0 && p[j] > temp; j -= gap)
        p[j + gap] = p[j];
      p[j + gap] = temp;
    }
  }
}

代码不算难理解, 核心还是插入排序, 只要我们弄懂了插入排序, 希尔排序就不在话下了.

对于空间复杂度, 这里不难理解, 肯定是O(1), 仅用于交换.

对于时间复杂度, 这里有点不太好解释, 我自己也没完全懂(笑), 就不在这里不懂装懂了, 贴一下结论:

归并排序

  • 介绍: 归并排序是采用分治法的一个很好的例子, 归并排序的思想就是先递归分解数组, 再合并数组,
    先考虑合并两个有序数组，基本思路是比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直至一个数组为空，最后把另一个数组的剩余部分复制过来即可。

再考虑递归分解，基本思路是将数组分解成左半边和右半边，如果这两个数组内部数据是有序的，那么就可以用上面合并数组的方法将这两个数组合并排序。
如何让这两个数组内部是有序的？可以再二分，直至分解出的小组只含有一个元素时为止，此时认为该小组内部已有序。然后合并排序相邻二个小组即可。

下面再贴一个图来帮助理解: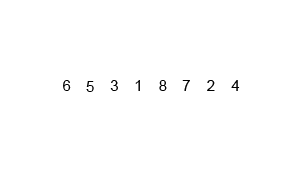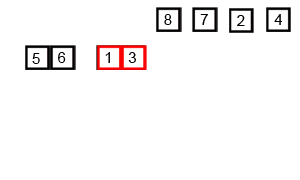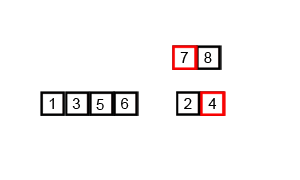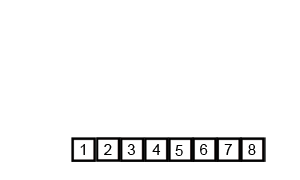gif

代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void mergeSortRecursively(int arr[], int reg[], int start, int end) {
  if (start >= end)
    return;
  int lenth = end - start;
  int mid = (lenth >> 1) + start;
  int start1 = start, end1 = mid;
  int start2 = mid + 1, end2 = end;
  mergeSortRecursively(arr, reg, start1, end1);
  mergeSortRecursively(arr, reg, start2, end2);
  int k = start;
  while (start1 <= end1 && start2 <= end2)
    reg[k++] = arr[start1] > arr[start2] ? arr[start2++] : arr[start1++];
  while (start1 <= end1)
    reg[k++] = arr[start1++];
  while (start2 <= end2)
    reg[k++] = arr[start2++];
  for (k = start; k <= end; ++k)
    arr[k] = reg[k];
}
void mergeSort(int *p, const int Length) {
  if (p == nullptr || Length <= 0)
    return;
  int *reg = new int[Length];
  mergeSortRecursively(p, reg, 0, Length - 1);
  delete[] reg;
}

这里定义了一个辅助的递归函数, 同样用迭代也可以写出归并排序的算法, 不过这里我个人倾向于用递归来实现, 因为递归实现的话代码比较简单, 逻辑比较清晰, 如果是面试的时候, 必然是优先选择递归算法而不是迭代算法了.

至于空间复杂度, 这里从代码中比较容易看出来是O(n), 需要一个与原数组大小相同的数组来作为辅助空间.

而时间复杂度的话, 就比较明显了, 因为使用的类似与二分法的方式, 所以时间复杂度很明显是O(nlogn), 而且不论是最好情况还是最坏情况下都是这个复杂度, 因为这个算法很明显对数组内数字是没有要求的. 稳定性的话, 算法是明显稳定的, 因为我们在遇到两个相同的数字的时候, 仍然是按先后顺序来放置数字的, 所以算法是稳定的.

快速排序

  • 介绍:快速排序这里我就不再介绍了, 我以前的一篇博客里面已经写过了快排的代码以及分析:快速排序理解

堆排序

  • 介绍:堆排序在top K问题中使用比较频繁.虽然我们在理解堆排序的时候用的是二叉堆的数据结构来实现的, 但是实质上是我们用的还是一维数组.二叉堆是一个近似完全二叉树

二叉堆有以下性质:

  1. 父节点的键值总是大于或者等于(小于等于)任何一个子节点的键值.
  2. 每个节点的左右子树都是一个二叉堆(都是最大堆或者最小堆).
    思路也不是很难理解, 步骤如下:
    1. 构造最大堆:若数组下标范围为0~n，考虑到单独一个元素是大根堆，则从下标n/2开始的元素均为大根堆, 这里用到了二叉堆的一个性质, 由于是近似完全二叉树, 所以下标大于等于n/2的节点偶都是叶子节点。于是只要从n/2-1开始，向前依次构造大根堆，这样就能保证，构造到某个节点时，它的左右子树都已经是大根堆。不过需要注意的是, 在构造最大堆的时候要注意保持其子树也仍然是最大堆, 这个时候就需要向下调整.
    2. 堆排序: 由于我们的堆是用数组模拟的, 得到一个最大堆之后, 数组内部并不是有序的, 因此需要将堆化数组有序化. 我们的思路是移除根节点, 并对最大堆的调整做递归运算. 第一次将heap[0]与heap[n-1]交换，再对heap[0…n-2]做最大堆调整。因为heap[0]是堆的根节点, 是整个数组中最大的数字, 交换之后就相当于最大数字已经”归位”了.第二次将heap[0]与heap[n-2]交换，再对heap[0…n-3]做最大堆调整。重复该操作直至heap[0]和heap[1]交换。由于每次都是将最大的数并入到后面的有序区间，故操作完后整个数组就是有序的了。
    3. 最大堆调整: 这就是上面我们说的构造最大堆, 目的是调整整个树, 使得子节点永远小于父节点.
      下面再上一个gif方便理解, 图片来自网络:gif
      代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void max_heapify(int *arr, int start, int end) {
  int dad = start;
  int son = dad * 2 + 1;
  while (son <= end) {
    if (son + 1 <= end && arr[son] < arr[son + 1])
      son++;
    if (arr[dad] > arr[son])
      return;
    else //交换之后注意要向下调整
    {
      std::swap(arr[dad], arr[son]);
      dad = son;
      son = dad * 2 + 1;
    }
  }
}
void heapSort(int *arr, const int length) {
  for (int i = (length >> 1) - 1; i >= 0; i--) {
    max_heapify(arr, i, length - 1);
  }
  for (int i = length - 1; i > 0; i--) {
    std::swap(arr[0], arr[i]);
    max_heapify(arr, 0, i - 1);
  }
}

对于空间复杂度, 很显然是O(1), 用于交换的.

对于时间复杂度, 我们将时间复杂度分为两个部分:
1. 建立最大堆:从最后一个非叶子节点开始把每一对二叉树元素（一个父节点和其子节点）进行构造堆操作（即如果左子节点和有子节点中的最大值比父节点更大，就与父节点交换以保证父节点最大，并且对以该子节点为根的二叉树元素继续递归上述操作以保证交换后的二叉树仍然是堆（即满足第二个条件）），一直往前进行到顶层的二叉树元素为止。 最终得到的堆即为最大堆。 以上操作复杂度为O(n)，大概需进行n/2 * 2 = n次比较和n/2次交换。
2. 更改堆之后重新建堆的时间是nlog(n), 更改之后重新建堆需要循环n-1次, 每次的调整时间是log(n)(因为是从根节点向下调整, 时间相当于是二叉树搜索),

综上来看, 时间复杂度为O(nlog(n)).稳定性的话, 很显然堆排序是不稳定的, 我们在这里就不再赘述了, 有兴趣的同学可以画个图理解一下.

总结: 到这里, 七个经典的排序算法就算是总结完了, 下面再上一张图, 总结了各个排序方法的各个指标:image